ข้ามไปที่เนื้อหาหลัก

เซต (Set) การแก้ปัญหาเกี่ยวกับเซต

 เซต (Set) 

การแก้ปัญหาเกี่ยวกับเซต


n(A∪B) = n(A) + n(B) เมื่อ A∩B = ø

n(A∪B) = n(A) + n(B) - n(A∩B) 

n(A∪B∪C) = n(A) + n(B) + n(C) - n(A∩B) - n(A∩C) - n(B∩C) + n(A∩B∩C) 


ตัวอย่างการแก้โจทย์ปัญหา

ผลสอบของนักเรียนห้องหนึ่ง จำนวน 40 คน ปรากฏว่า สอบผ่านวิชาคณิตศาสตร์ 18 คน สอบผ่านวิชาภาษาอังกฤษ 26 คน และผ่านทั้งสองวิชา 10 คน จงหาจำนวนนักเรียนที่สอบผ่านทั้งหมด และนักเรียนที่สอบไม่ผ่านทั้งหมด

ให้   U = จำนวนนักเรียนทั้งหมด

 A = นักเรียนที่สอบผ่านวิชาคณิตศาสตร์

        B = นักเรียนที่สอบผ่านวิชาภาษาอังกฤษ

หาคำตอบโดยการใช้สูตร ดังนี้

จะได้ n(A) = 18, n(B) = 26, n(A∩B) = 10
จากสูตร n(A∪B) = n(A) + n(B) - n(A∩B)
แทนค่า  n(A∪B) = 18 + 26 - 10
  = 34
ดังนั้น มีนักเรียนที่สอบผ่านทั้งหมด 34 คน
จะได้ นักเรียนที่สอบไม่ผ่านทั้งหมด = n(U) - n(A∪B)
   = 40 - 34 
   = 6 

ดังนั้น มีนักเรียนที่สอบไม่ผ่านทั้งหมด 6 คน

หาคำตอบโดยการใช้แผนภาพ ดังนี้


n(A∪B) = 8 + 10 + 16
   = 34

ดังนั้น มีนักเรียนที่สอบผ่านทั้งหมด 34 คน

จะได้ นักเรียนที่สอบไม่ผ่านทั้งหมด = n(U) - n(A∪B)
   = 40 - 34 
   = 6 

ดังนั้น มีนักเรียนที่สอบไม่ผ่านทั้งหมด 6 คน

 

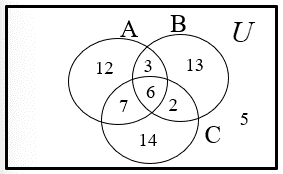
ในการสำรวจความชอบรับประทานผลไม้ 3 อย่าง ของนักเรียนห้องหนึ่ง จำนวน 62 คน พบว่า ชอบส้ม 28 คน แตงโม 24 คน มังคุด 29 คน ชอบส้มและแตงโม 13 คน ส้มและมังคุด 12 คน แตงโมและมังคุด 14 คน ชอบทั้งสามอย่าง 6 คน จงหาคนที่ไม่ชอบทั้งสามอย่าง

ให้   U = จำนวนนักเรียนทั้งหมด

 A = นักเรียนที่ชอบส้ม 

         B = นักเรียนที่ชอบแตงโม

C = นักเรียนที่ชอบมังคุด

หาคำตอบโดยการใช้สูตร ดังนี้

จะได้ n(U) = 62, n(A) = 28, n(B) = 24, n(C) = 29, n(A∩B) = 9 , n(A∩C) = 13, n(B∩C) = 8, n(A∩B∩C) = 6
จากสูตร n(A∪B∪C) = n(A) + n(B) + n(C) - n(A∩B) - n(A∩C) - n(B∩C) - n(A∩B∩C)
แทนค่า  n(A∪B∪C) = 28 + 24 + 29 - 9 - 13 - 8 + 6
      = 57
นักเรียนที่ไม่ชอบผลไม้ทั้งสามอย่าง = n(U) - n(A∪B∪C)
นักเรียนที่ไม่ชอบผลไม้ทั้งสามอย่าง = 62 - 57 
    = 5
ดังนั้น มีนักเรียนที่ไม่ชอบผลไม้ทั้งสามอย่าง 5 คน

หาคำตอบโดยการใช้แผนภาพ ดังนี้



นักเรียนที่ไม่ชอบผลไม้ทั้งสามอย่าง = n(U) - n(A∪B∪C)
  = 62 - (12 + 7 + 3 + 6 + 2 + 13 + 14)
      = 62 - 57 
      = 5
ดังนั้น มีนักเรียนที่ไม่ชอบผลไม้ทั้งสามอย่าง 5 คน

 ฝึกสมอง ลองความไว กับแอป QMath เล่นง่าย สนุกกับการเรียนรู้ สามารถดาวน์โหลดแอปได้ที่ลิงค์ด้านล่างเลยนะคะ

https://play.google.com/store/apps/details?id=com.pro45.qmath

ป้ายกำกับ:

ความคิดเห็น

แสดงความคิดเห็น

โพสต์ยอดนิยมจากบล็อกนี้

ปริมาตรปริซึม

ปริมาตรปริซึม ตัวอย่างการคำนวณปริมาตรปริซึม      ปริซึมสี่เหลี่ยมรูปหนึ่ง กว้าง 4 เซ็นติเมตร ยาว 8 เซ็นติเมตร และสูง 15 เซ็นติเมตร  จงหาปริมาตรปริซึมสี่เหลี่ยมรูปนี้       วิธีทำ               จากสูตรการหาปริมาตรของปริซึม = พื้นที่ฐาน x สูง               จากรูป ฐานของรูปปริซึมสี่เหลี่ยมรูปนี้เป็นรูปสี่เหลี่ยมผืนผ้า กว้าง 4 cm. และยาว 8 cm.               ดังนั้น พื้นที่ฐานรูปสี่เหลี่ยมผืนผ้า = ก x ย               แทนค่าตามสูตรปริมาตรปริซึม = พื้นที่ฐาน x สูง                                                       = ก x ย x ส                                                       = 4 x 8 x 15                                                       = 480        ตอบ ปริซึมสี่เหลี่ยมรูปนี้มีปริมาตร คือ 480 ลูกบาศก์เซ็นติเมตร     ปริซึมสามเหลี่ยมรูปหนึ่ง สูง 15 เซ็นติเมตร มีความยาวฐาน 6 เซ็นติเมตร และส่วนสูงของฐาน 5  เซ็นติเมตร  จงหาปริมาตรปริซึมสามเหลี่ยมรูปนี้       วิธีทำ               จากสูตรการหาปริมาตรของปริซึม = พื้นที่ฐาน x สูง               จาก
แสดงความคิดเห็น
อ่านเพิ่มเติม

เลขยกกำลัง ตัวอย่าง 5 (math logarithm)

คำถาม จงเขียนจำนวนต่อไปนี้ในรูปเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มที่มากกว่า 1   พร้อมทั้งบอกฐาน และเลขชี้กำลัง                          0.0025 เขียนในรูปเลขยกกำลัง คือ …………………………………… ฐาน  คือ.................................................................................... เลขชี้กำลัง คือ ...……………………………………………… ตอบ เขียนในรูปเลขยกกำลัง คือ   0.05 2 ฐาน  คือ     0.05 เลขชี้กำลัง คือ    2
แสดงความคิดเห็น
อ่านเพิ่มเติม

ประพจน์ (Propositions หรือ Statements)

ประพจน์ ( Propositions  หรือ Statements ) ประพจน์  คือ  ประโยคหรือข้อความที่เป็นจริงหรือเท็จ อย่างใดอย่างหนึ่งเท่านั้น ประโยคหรือข้อความที่มีลักษณะดังกล่าวจะอยู่ในรูปบอกเล่าหรือปฏิเสธก็ได้ ตัวอย่างประโยคหรือข้อความที่เป็นประพจน์             1.   สกลนครเป็นจังหวัดที่อยู่ทางภาคเหนือของไทย               (เท็จ)             2.  2 + 3 = 5                                                                             (จริง)             3.  แมวเป็นสัตว์ที่มีสองขา                                                      (เท็จ)             4.  เดือนมิถุนายนมี 30 วัน                                                        (จริง)             5.  9 หารด้วย 3 ลงตัว                                                              (จริง) จากตัวอย่างข้างต้น  การเป็นจริงหรือเท็จ (true or false)ในทางตรรกศาสตร์   ของแต่ละประพจน์   เรียกว่า   ค่าความจริงของประพจน์ (truth - value) ข้อความที่ไม่ได้อยู่ในรูปบอกเล่าหรือปฏิเสธ จะไม่เป็นประพจน์  เช่น  ประโยคคำถา
แสดงความคิดเห็น
อ่านเพิ่มเติม